The rule of 17 in volleyball

Scott Adams, the author of Dilbert, writes in his book “How to Fail at Almost Everything and Still Win Big”:

Recently I noticed that the high-school volleyball games I attended in my role as stepdad were almost always won by the team that reached seventeen first, even though the winning score is twenty-five and you have to win by two.

It’s common for the lead to change often during a volleyball match, and the team that first reaches seventeen might fall behind a few more times before winning, which makes the pattern extra strange.

Good observation, Scott! But why could it be so?

Scott offers two possible explanations. One is psychological: the leading team has a higher morale while the losing team feels defeated. The other is that perhaps the coach of the losing team sees this as an opportunity to let his bench players on the court.

While these reasons sound plausible to me, there is a simpler logical explanation. It would hold even if the players and coaches were robots.

Imagine that you enter a gym where a game is being played. You see the current score: 15:17. If you know nothing else about the teams except their current score, which one do you think is more likely to win the set?

There are two reasons to think it is the leading team:

1. The score by itself doesn’t offer much evidence that the leading team is stronger or in a better shape. However, if one of the teams is stronger, it is more likely to be the leading team.
2. Even without assuming anything about how good the teams are, the leading team at this moment is up for an easier task: it needs only 8 points to win, whereas the team behind needs 10 points.

To quantify the reliability of Scott Adams’s “rule of 17”, I wrote a simple simulation in R:

sim.one <- function(prob, threshold) {
  score <- c(0,0)
  leader <- NA
  serving <- 1
  while (all(score < 25) || abs(diff(score)) < 2) {
    winner <-
      if (as.logical(rbinom(1,1,prob[[serving]])))
        serving
      else
        3 - serving
    score[[winner]] <- score[[winner]] + 1
    serving <- winner
    if (is.na(leader) && any(score == threshold)) {
      leader <- which.max(score)
    }
  }
  return(c(leader, which.max(score)))
}

Here prob is a 2-dimensional vector \((p_1,p_2)\), where \(p_i\) is the probability of team \(i\) to win their serve against the opposing team. The function simulates a single set and returns two numbers: which team first scored threshold (e.g. 17) points and which team eventually won. If the two numbers are equal, the rule worked in this game.

Then I simulated a game 1000 times for each of many combinations of \(p_1\) and \(p_2\) and calculated the fraction of the games where the rule worked. Here’s the result:

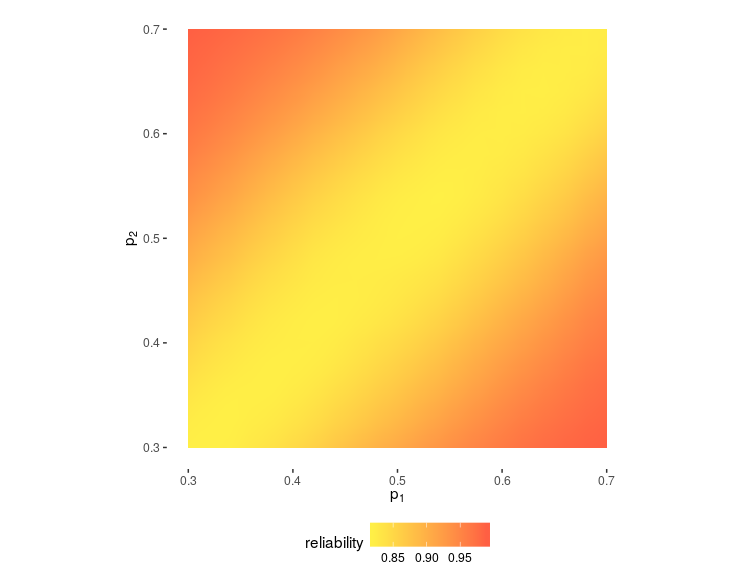
When \(p_1=p_2\), the reliability of the rule is independent of the values of \(p_1\) and \(p_2\) (within the tested limits of \(0.3\) and \(0.7\)) and equals approximately \(81\%\). This is entirely due to reason 2: all else being equal, the leading team has a head start.

When teams are unequal, reason 1 kicks in, and for large inequalities, the reliability of the rule approaches \(1\). For instance, when \(p_1=0.3\) and \(p_2=0.7\), the rule works about \(99\%\) of the time.

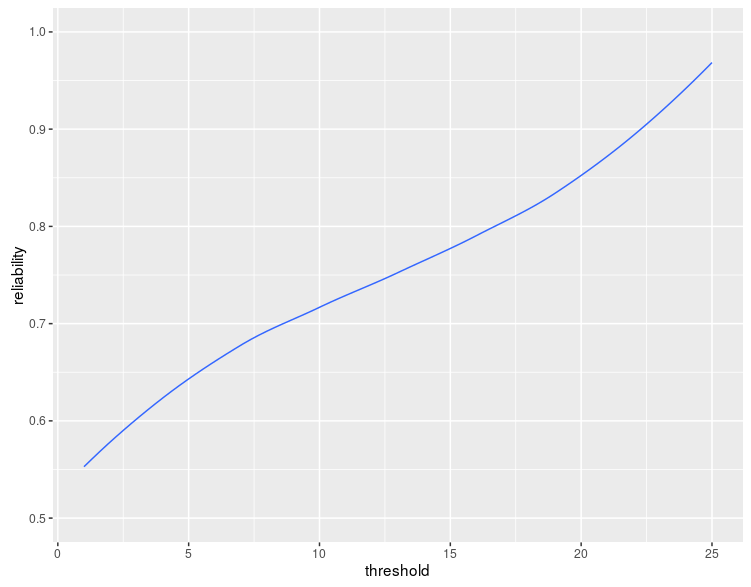
Is there anything magical about the number 17? No, we would expect the rule to work for any threshold at least to some extent. The reliability would grow from somewhere around \(50\%\) for the threshold of \(1\) to almost \(100\%\) for the threshold of \(25\).

And indeed, this is what we observe (for \(p_1=p_2\)):

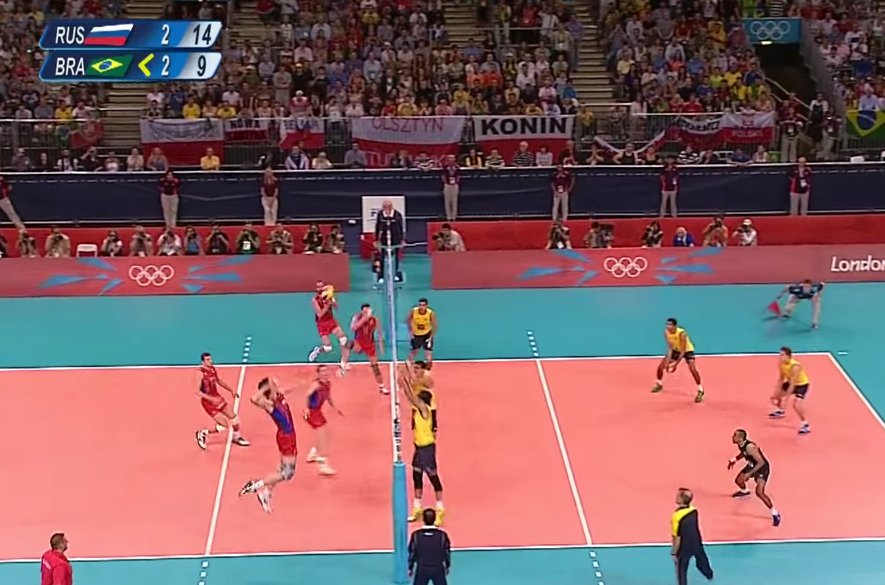
This reminds me of men’s gold medal match at the 2012 London Olympics, where Russia played against Brazil. Russia loses the first two sets. A game lasts until one of the teams wins 3 sets in total, so Russia cannot afford to lose a single set now. In the third set, Brazil continues to lead, reaching 17 (and then 18) points while Russia has 15. Several minutes later, Brazil leads 22:19.

And then, against all odds, the Russian team wins that set 29:27, then the two following sets, and gets the gold.