Descending sort in Haskell

When confronted with a problem of sorting a list in descending order in Haskell, it is tempting to reach for a “lazy” solution reverse . sort.

An obvious issue with this is efficiency. While sorting in descending order should in theory be exactly as efficient as sorting in ascending order, the above solution requires an extra list traversal after the sorting itself is done.

This argument can be dismissed on the grounds that reverse’s run time, \(\Theta(n)\), is, in general, less than sort’s run time, \(O(n \log n)\), so it’s not a big deal. Additionally, one could argue that, unlike more complex solutions, this one is “obviously correct”.

As the rest of this article explains, neither of these claims holds universally.

Proper solutions

Here are the two ways to sort a list in descending order that I am aware of. Both require the more general sortBy function

sortBy :: (a -> a -> Ordering) -> [a] -> [a]

The first argument to sortBy is the comparison function. For each pair of arguments it returns a value of type

data Ordering = LT | EQ | GT

which describes the ordering of those arguments.

The “standard” ordering is given by the compare function from the Ord typeclass. Thus, sort is nothing more than

sort = sortBy compare

The first solution to the descending sort problem exploits the fact that, to get the opposite ordering, we can simply swap around the two arguments to compare:

sortDesc = sortBy (flip compare)

The second solution relies on the comparing function from Data.Ord, which gives a particular way to compare two values: map them to other values which are then compared using the standard Ord ordering.

comparing :: Ord a => (b -> a) -> b -> b -> Ordering

This trick is often used in mathematics: to maximize a function \(x\mapsto f(x)\), it suffices to minimize the function \(x \mapsto -f(x)\). In Haskell, we could write

sortDesc = sortBy (comparing negate)

and it would work most of the time. However,

> sortDesc [1,minBound::Int]
[-9223372036854775808,1]

Besides, negation only works on numbers; what if you want to sort a list of pairs of numbers?

Fortunately, Data.Ord defines a Down newtype which does exactly what we want: it reverses the ordering between values that it’s applied to.

> 1 < 2
True
> Down 1 < Down 2
False

Thus, the second way to sort the list in descending order is

sortDesc = sortBy (comparing Down)

sortOn

Christopher King points out that the last example may be simplified with the help of the sortOn function introduced in base 4.8 (GHC 7.10):

sortOn :: Ord b => (a -> b) -> [a] -> [a]

Thus, we can write

sortDesc = sortOn Down

Very elegant, but let’s look at how sortOn is implemented:

sortOn f =
  map snd .
  sortBy (comparing fst) .
  map (\x -> let y = f x in y `seq` (y, x))

This is somewhat more complicated than sortBy (comparing Down), and it does the extra work of first allocating \(n\) cons cells and \(n\) tuples, then allocating another \(n\) cons cells for the final result.

Thus, we might expect that sortOn performs worse than sortBy. Let’s check our intuition:

import Criterion
import Criterion.Main
import Data.List
import Data.Ord

list :: [Int]
list = [1..10000]

main = defaultMain
  [ bench "sort"   $ nf sort (reverse list)
  , bench "sortBy" $ nf (sortBy (comparing Down)) list
  , bench "sortOn" $ nf (sortOn Down) list
  ]

(Why reverse?)

benchmarking sort
time                 134.9 μs   (134.3 μs .. 135.4 μs)
                     1.000 R²   (0.999 R² .. 1.000 R²)
mean                 134.8 μs   (134.2 μs .. 135.7 μs)
std dev              2.677 μs   (1.762 μs .. 3.956 μs)
variance introduced by outliers: 14% (moderately inflated)

benchmarking sortBy
time                 131.0 μs   (130.6 μs .. 131.4 μs)
                     1.000 R²   (1.000 R² .. 1.000 R²)
mean                 131.1 μs   (130.8 μs .. 131.4 μs)
std dev              965.1 ns   (766.5 ns .. 1.252 μs)

benchmarking sortOn
time                 940.5 μs   (928.6 μs .. 958.1 μs)
                     0.998 R²   (0.997 R² .. 0.999 R²)
mean                 950.6 μs   (940.9 μs .. 961.1 μs)
std dev              34.88 μs   (30.06 μs .. 44.19 μs)
variance introduced by outliers: 27% (moderately inflated)

As we see, sortOn is 7 times slower than sortBy in this example. I also included sort in this comparison to show that sortBy (comparing Down) has no runtime overhead.

There is a good reason why sortOn is implemented in that way. To quote the documentation:

sortOn f is equivalent to sortBy (comparing f), but has the performance advantage of only evaluating f once for each element in the input list. This is called the decorate-sort-undecorate paradigm, or Schwartzian transform.

Indeed, if f performed any non-trivial amount of work, it would be wise to cache its results—and that’s what sortOn does.

But Down is a newtype constructor—it performs literally no work at all—so the caching effort is wasted.

sortWith

Yuriy Syrovetskiy points out that there is also sortWith defined in GHC.Exts, which has the same type as sortOn but does no caching. So if you want to abbreviate sortBy (comparing Down), you can say sortWith Down—but you need to import GHC.Exts first.

Wonder why sortWith lives in GHC.Exts and not in Data.List or Data.Ord? It was originally added to aid writing SQL-like queries in Haskell, although I haven’t seen it used a single time in my career.

Asymptotics

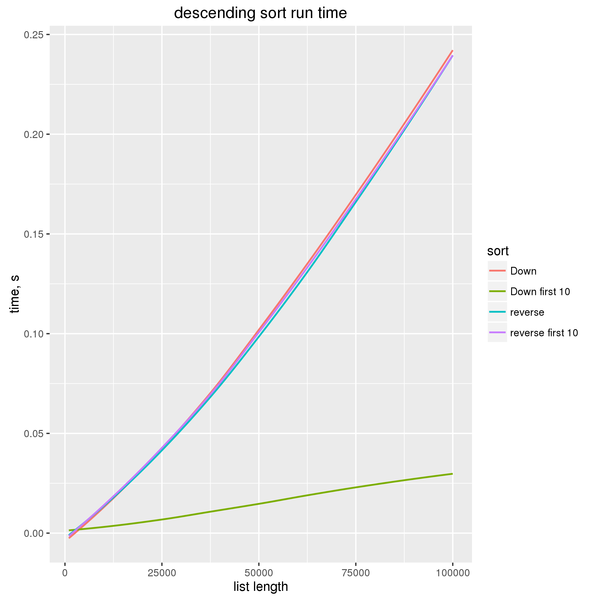
Thanks to Haskell’s laziness in general and the careful implementation of sort in particular, sort can run in linear time when only a fixed number of first elements is requested.

So this function will return the 10 largest elements in \(\Theta(n)\) time:

take 10 . sortBy (comparing Down)

While our “lazy” solution

take 10 . reverse . sort

(which, ironically, turns out not to be lazy enough—in the technical sense of the word “lazy”) will run in \(O(n \log n)\) time. This is because it requests the last 10 elements of the sorted list, and in the process of doing so needs to traverse the whole sorted list.

This may appear paradoxical if considered outside of the context of lazy evaluation. Normally, if two linear steps are performed sequentially, the result is still linear. Here we see that adding a linear step upgrades the overall complexity to \(O(n \log n)\).

Semantics

As I mentioned in the beginning, the simplicity of reverse . sort may be deceptive. The semantics of reverse . sort and sortBy (comparing Down) differ in a subtle way, and you probably want the semantics of sortBy (comparing Down).

This is because sort and sortBy are stable sorting functions. They preserve the relative ordering of “equal” elements within the list. Often this doesn’t matter because you cannot tell equal elements apart anyway.

It starts to matter when you use comparing to sort objects by a certain feature. Here we sort the list of pairs by their first elements in descending order:

> sortBy (comparing (Down . fst)) [(1,'a'),(2,'b'),(2,'c')]
[(2,'b'),(2,'c'),(1,'a')]

According to our criterion, the elements (2,'b') and (2,'c') are considered equal, but we can see that their ordering has been preserved.

The revese-based solution, on the other hand, reverses the order of equal elements, too:

> (reverse . sortBy (comparing fst)) [(1,'a'),(2,'b'),(2,'c')]
[(2,'c'),(2,'b'),(1,'a')]

Sort with care!

A note on sorted lists

The original version of this article said that sort runs in \(\Theta(n \log n)\) time. @obadzz points out that this is not true: sort is implemented in such a way that it will run linearly when the list is already almost sorted in any direction. Thus I have replaced \(\Theta(n \log n)\) with \(O(n \log n)\) when talking about sort’s complexity.

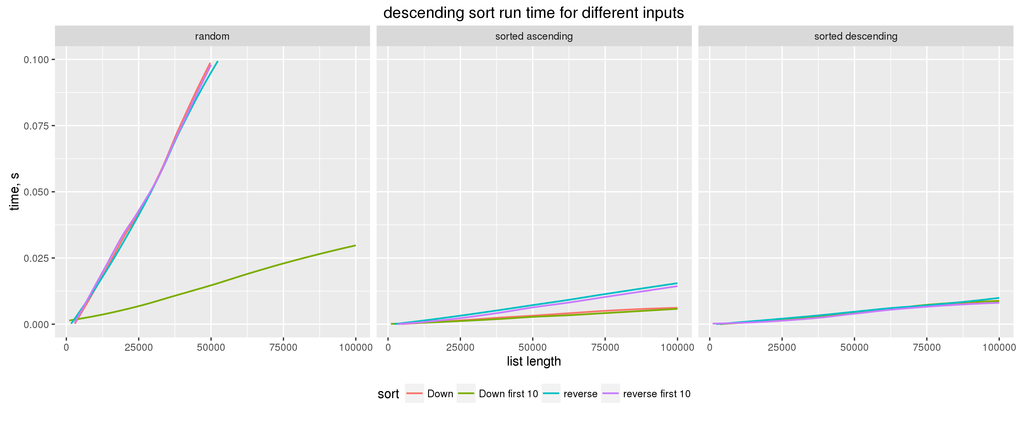
Why reverse in the benchmark?

Jens Petersen asks why in the benchmark above I’m comparing

nf (sortBy (comparing Down)) list

to

nf sort (reverse list)

I include sort here as a baseline, to demonstrate that sortBy (comparing Down) does not have any significant overhead comparing to a simple sort. But why have reverse there? Is that a typo?

First of all, it’s important to understand what

nf sort (reverse list)

does. It may look as if it’s measuring the time it takes to reverse and then sort a list—and why would anyone want to do such a thing?

But that’s not what’s happening. In criterion, the nf combinator takes two separate values: the function (here, sort) and its argument (here, (reverse list)). Both the function and the argument are precomputed, and what’s measured repeatedly is the time it takes to evaluate the application of the function to its argument.

The reason I measure the time it takes to sort the reversed list is to have more of an apples-to-apples comparison. If I compared

nf (sortBy (comparing Down)) list

to

nf sort (reverse list)

… I would be comparing the same algorithm but on the arguments on which it takes two different code paths: in one case it ends up reversing the list, in the other keeping it intact. (Counterintuitively, it looks like it’s faster for sort/sortBy to reverse the list than to keep it as-is.)

Therefore, by reversing the argument, I make sure that in all three cases (sort, sortBy, and sortOn) the input list “looks” the same as seen by the comparison function, and in all three cases the sorting algorithm needs to reverse the list.